물체가 회전하면 그 방향이 바뀐다.
11. 1 오일러 변환
오일러 변환(Euler transform)
- 세 개의 주축 중심 회전을 결합한 것
- 주축은 월드 공간에서 선택할 수 있고, 오브젝트 공간에서 선택할 수 있다.
11.1.1 월드 공간 오일러 변환

위 사진들은 월드 공간의 주축을 중심으로 회전한 것이다.
오일러 각(Euler angles)
세 축 중심의 회전각 $\theta_1$, $\theta_2$, $\theta_3$을 가리킴
오일러 변환은 순서를 다르게 하면 결과가 다르게 나온다.
11.1.2 오브젝트 공간 오일러 변환
물체가 움직이면 그 오브젝트 공간도 같이 움직인다.
월드 공간에서의 오일러 변환에 사용한 오일러 각을 오브젝트 공간에서의 오일러 변환에 사용하면 결과는 다르게 나온다. 왜냐하면 오브젝트 공간에서의 오일러 변환은 축도 같이 움직이기 때문이다.
오브젝트 공간 오일러 변환은 월드 공간 주축을 대신 사용하되 그 순서를 거꾸로 하는 것으로도 볼 수 있다.
ex) $ R_n\left(\theta_3\right)R_v\left(\theta_2\right)R_u\left(\theta_1\right)
= R_x\left(\theta_1\right)R_y\left(\theta_2\right)R_z\left(\theta_3\right)$
11.2 키 프레임 애니메이션과 오일러 변환
애니메이터가 애니메이션 패키지를 사용해 제작한 일련의 동작은 런타임에 재생된다.
애니메이터는 모든 프레임(frame)에서의 동작을 정의하진 않는다.
예를 들어, 60 fps 애니메이션의 경우에는 1초에 60보다 훨씬 적은 수의 프레임에 대해서만 동작을 정의한다.
이를 카리켜 키프레임(keyframe)이라 부른다. 키프레임 사이의 중간 프레임(in-between frame)은 런타임에 자동으로 채워진다.
11.2.1 2차원 프레임 애니메이션
키 데이터(key data)
- 키프레임에 할당된 중요 데이터

중간 프레임에서는 이러한 키 데이터가 보간되는데, 시간에 따라 변하는 모든 데이터는 모두 보간 대상이 된다. ex) 위치, 방향, 축소확대 인자 등
11.2.2 3차원 키프레임 애니메이션
2차원 키프레임 애니메이션에서의 개념은 3차원에 그대로 적용된다.
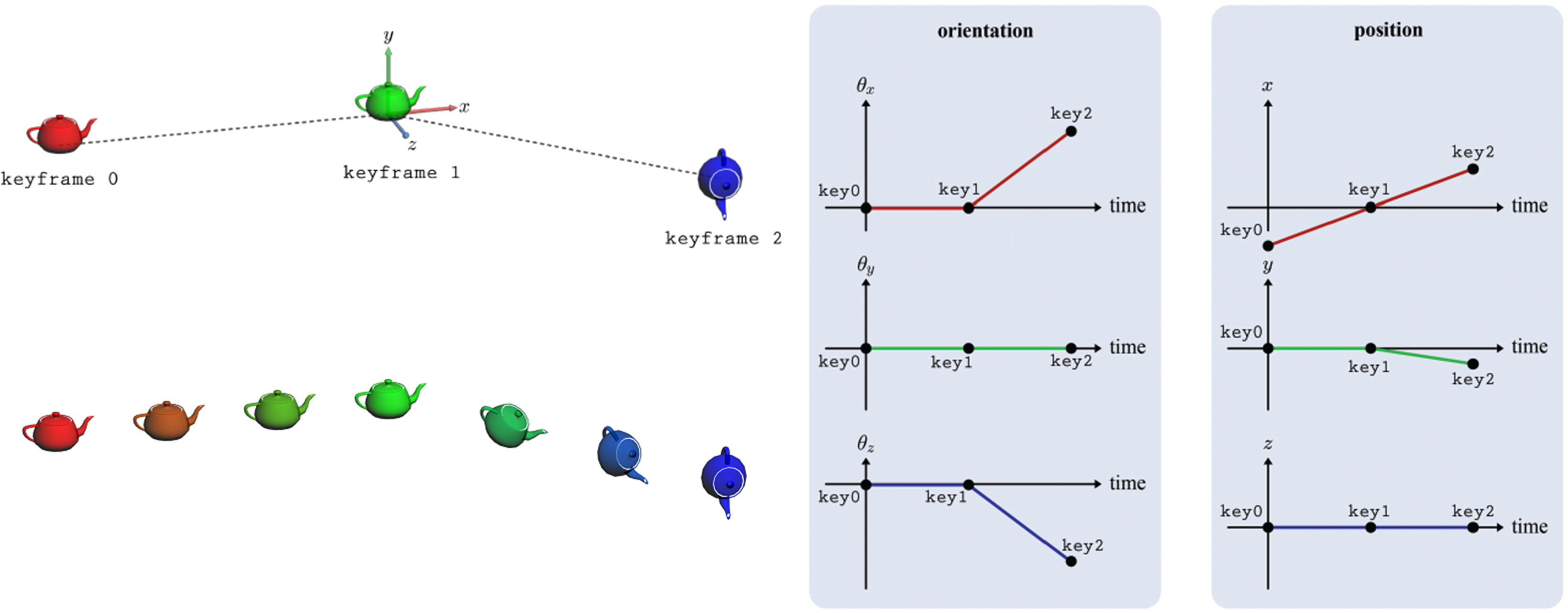
우측에 있는 그래프에서 검은 점은 키데이터이다. 이들을 잇는 선분은 키 데이터를 선형보간했음을 의미한다.
중간 프레임에서 주전자의 $\left( \theta_x, \theta_y, \theta_z \right)$와 $\left( x, y, z \right)$를 얻기 위해서는 그래프를 동일한 시간에서 샘플링하면 된다. 이렇게 얻어진 위치 및 방향 데이터를 잉요해 주전자를 렌더링한다.
위 그림을 보면 색상도 보간되었음을 알 수 있다.

일반적으로 모델링 및 애니메이션 패키지는 그래픽 인터페이스를 통해 위 사진에서의 그래프를 애니메이터에게 제공하고 그래프를 편집할 수 있게 한다.
편집 과정에서 키 데이터를 수정할 수 있고, 선형보간 대신 고차원 보간을 선택할 수도 있고 보간 곡선의 모양을 변경할 수도 있다.
11.2.3 오일러 각의 보간
물체의 방향을 정의하는 데 있어 오일러 각 $ \left( \theta_1, \theta_2, \theta_3 \right)$는 매우 직관적인 수단을 제공한다.
하지만, 오일러 각의 한계 중 하나는 올바르게 보간된다는 보장이 없다는 것이다.

t=0.5인 중간 프레임에서의 방향을 계산해 보면 그 결과는 $\left( 45^{\circ}, 67.5^{\circ} , 45^{\circ} \right)$이다.
(c)는 오일러 각을 연속적으로 적용한 결과를 보여준다. L자형 물체는 yz평면에 놓여있지 않다.
두 키프레임의 물체가 yz평면에 놓여있기 때문에 중간 프레임의 물체도 그렇게 되어야 하는데, 오일러 각 보간은 예기치 않은 결과를 낳은 것이다.
오일러 각은 올바르게 보간된다는 보장이 없기 때문에, 보간을 핵심 기능으로 가지는 키프레임 애니메이션에 적합하지 않다. 반면, 임의의 방향이나 회전을 표현하는 또 다른 기법인 쿼터니언(quaternion)은 항상 올바르게 보간된다.
11.3 쿼터니언
11.3.1 쿼터니언 표현
쿼터니언은 복소수를 확장한 것으로 다음과 같이 네 개의 항으로 표현된다.

$q_x$, $q_y$, $q_z$는 허수부(imaginary part)를 구성하고, $q_w$는 실수부(real part)인데, $i, j, k$를 허수단위(imaginary unity)라 한다. 허수부는 종종 $\mathbf{q}_v$로 줄여쓴다. 따라서 쿼터니언은 $\left(\mathbf{q}_v, q_w\right)$로 표현하기도 한다.
허수단위는 다음과 같은 특징을 가진다.
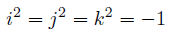
두 개의 서로 다른 허수단위가 곱해지면, 순환치환(cyclic permutation)적인 특징을 가진다.

두 개의 쿼터니언 $\left( p_x, p_y, p_z, p_w \right)$와 $\left( q_x, q_y, q_z, q_w \right)$를 각각 $\mathbf{p}$와 $\mathbf{q}$로 표기하면, 둘의 곱은 다음과 같이 계산된다.

일반 복소수처럼 쿼터니언도 켤레(conjugate)를 가진다.

두 개의 쿼터니언 $\mathbf{p}$와 $\mathbf{q}$에 대해 $\left(\mathbf{p} \mathbf{q}\right)^* = \mathbf{q}^* \mathbf{p}^*$이다.
쿼터니언의 크기(norm)는 일반적인 벡터의 경우와 같은 방법으로 계산된다.
$\left\| \mathbf{q} \right\| = \sqrt{{q_x}^2 + {q_y}^2 + {q_z}^2 + {q_w}^2 }$
만약 $\mathbf{q}$의 크기 즉 $\left\| \mathbf{q} \right\|$가 1이라면 $\mathbf{q}$는 단위 쿼터니언(unit quaternion)이라 불린다.
11.3.2 쿼터니언을 이용한 회전

$x$를 실수부로 $y$를 허수부로 가지는 복소수 $x+yi$를 $\mathbf{p}$라 하자.
한편, 회전각 $\theta$가 주어졌을 때, 이를 크기가 1인 극형식(polar form)의 복소수로 표현하면 $\cos{\theta} + \sin{\theta}i$가 된다. 이를 $\mathbf{q}$라 하자.
$\mathbf{p}$와 $\mathbf{q}$를 곱하면 다음과 같은 결과를 얻는다.

복소수의 실수부와 허수부는 $x'$ 및 $y'$와 일치함을 발견할 수 있다.
즉, 복소수를 이용하여 2차원 회전을 표현한 것
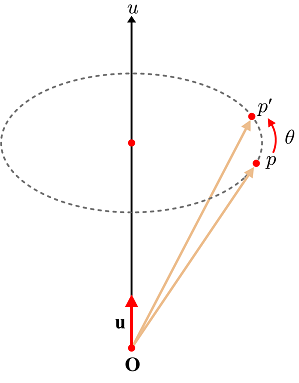
3차원 벡터 $p$를 $u$중심으로 $\theta$만큼 회전시키는 경우에, 회전할 벡터와 회전 변환 각각을 쿼터니언으로 표현하자. 우선 $p$를 쿼터니언 $\mathbf{p}$로 표현하면, $\mathbf{p}$의 허수부는 $p$ 허수부는 $p$가 되고 실수부는 0이 된다.

회전축 $u$와 회전각 $\theta$로 또 다른 쿼터니언 $\mathbf{q}$를 정의할 것인데, 회전을 표현하는 쿼터니언의 크기는 1이 되어야 한다.
이를 위해 먼저 $u$를 자신의 길이로 나누어 단위 벡터 $u$를 만든다.
그러면 크기가 1인 극형식의 쿼터니언은 다음과 같이 정의된다.

여기서 각도가 $\frac{\theta}{2}$인 이유)
이중 덮개(double cover): 하나의 물리적인 회전이 두 개의 수학적 표현으로 나타나는 것
쿼터니언의 특성상 q와 -q는 같은 회전을 나타낸다. 따라서 각도가 절반이 된다.
마지막으로 $p$를 $\mathbf{u}$(혹은 $u$) 중심으로 $\theta$만큼 회전하는 것은 다음과 같이 표현된다.
$\mathbf{p}' = \mathbf{qpq}^*$
두 개의 쿼터니언을 곱하면 새로운 쿼터니언이 된다. 위 식에서 $\mathbf{qp}$는 쿼터니언이다.
또 다른 쿼터니언인 $\mathbf{q}^*$를 곱하면 역시 쿼터니언이 된다. 즉 $\mathbf{p}'$는 쿼터니언이다.
$\mathbf{p}'$의 실수부는 0이지만, 허수부는 $p$의 회전 결과인 $p'$와 같게 된다.
참고
쿼터니언을 이용한 회전 - 증명
쿼터니언 $\mathbf{p}$와 $\mathbf{q}$를 각각 $\left( \mathbf{p}_v, p_w \right)$와 $\left( \mathbf{q}_v, q_w \right)$로 표기하면 $\mathbf{pq}$는 다음과 같이 고쳐 쓸 수 있다.

$\times$는 벡터곱, $\cdot$은 내적 의미

[1]은 $p_w$가 0(순수한 회전만 생각하므로 실수부가 0이다)이어서 얻어지는 결과다.
[2]는 위의 $\mathbf{pq}$를 고쳐 쓴 수식에서 유도한 결과다.
[3]의 허수부는 $\mathbf{a} \times \left(\mathbf{b} \times \mathbf{c}\right) = \left(\mathbf{a} \cdot \mathbf{c}\right)\mathbf{b} - \left(\mathbf{a} \cdot \mathbf{b}\right)\mathbf{c}$의 정리에 따라 얻고, 실수부가 0이 되는 이유는 $\left( \mathbf{q}_v \times \mathbf{p}_v \right) \cdot \mathbf{q}_v = 0$이기 때문이다.
[4]는 $\mathbf{q} = \left( \sin{\frac{\theta}{2}}\mathbf{u}, \cos{\frac{\theta}{2}} \right)$라는 정의를 사용한 결과다.
[5]는 $\sin^2\frac{\theta}{2} = \frac{1-\cos{\theta}}{2}, cos^2\frac{\theta}{2} = \frac{1+\cos\theta}{2}, \sin{2\theta} = 2\sin\theta\cos\theta$의 정리에 따라 얻어진다.
[6]은 [5]를 재구성하여 얻어진 결과다.

$p$가 원반 둘레를 따라 회전하여 $p'$로 변환되는 것을 보면, 원점 $\mathbf{O}$와 원반 중심을 잇는 벡터는 $\left( \mathbf{u} \cdot \mathbf{p}_v \right)\mathbf{u}$이다.
서로 직교하는 원반 위의 벡터 한쌍을 보면, 하나는 $\mathbf{u} \times \mathbf{p}_v$로, 다른 하나는 원반 중심과 $p$를 잇는 벡터 $\mathbf{p}_v - \left( \mathbf{u} \cdot \mathbf{p}_v \right)\mathbf{u}$로 설정할 수 있다.

위 사진은 원반을 위에서 바라본 것이다. $p'$는 $\cos\theta\left(\mathbf{p}_v-\left(\mathbf{u}\cdot\mathbf{p}_v\right)\mathbf{u}\right)$와 $\sin\theta\left( \mathbf{u} \times \mathbf{p}_v \right)$의 합이 된다.
여기에 원반 중심까지의 벡터 $\left( \mathbf{u} \cdot \mathbf{p}_v \right)\mathbf{u}$가 더해지면 $p'$의 최종 값을 얻는다.
바로 [6]의 허수부이다.
$\mathbf{p}'$는 회전 후 벡터 $p'$를 나타내는데, $p'$를 또 다른 쿼터니언 $\mathbf{r}$을 사용하여 회전시키는 경우를 생각해보면

$\mathbf{rq}$가 두 회전이 결합된 쿼터니언임을 보여준다.

위 사진은 $\mathbf{u}$를 중심으로 $\theta$만큼 회전하는 것은 $-\mathbf{u}$를 중심으로 $-\theta$만큼 회전하는 것과 같음을 보여준다. 이들을 각각 $\mathbf{q}$와 $\mathbf{r}$로 표현하면 다음과 같다.
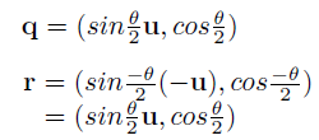
이는 $\mathbf{q}$와 $\mathbf{r}$이 동일한 쿼터니언임을 증명한다.
쿼터니언 $\mathbf{q}$는 '$\mathbf{u}$ 중심 $\theta$만큼 회전' 즉, $q = \left( \sin\frac{\theta}{2}\mathbf{u}, \cos\frac{\theta}{2} \right)$이고, $\mathbf{s}$는 '$\mathbf{u}$ 중심 $2\pi+\theta$만큼 회전'이라고 하자.
$q$와 $s$가 동일한 회전을 표현하는 것은 분명한데, $s$는 다음과 같이 정리될 수 있다.
이는 $\mathbf{q}$의 모든 원소의 부호를 바꾼 것이므로 $-\mathbf{q}$로 쓸 수 있다.
즉 $\mathbf{s} = -\mathbf{q}$의 관계가 성립한다. 따라서 $\mathbf{q} = -\mathbf{q}$이다.
즉 $\mathbf{q}$와 $-\mathbf{q}$는 동일한 회전을 표현한다.
11.3.3 쿼터니언의 보간
회전을 나타내는 두 개의 단위 쿼터니언 $\mathbf{q}$와 $\mathbf{r}$이 있다고 하면, [0, 1] 범위에서 정규화된 파라미터 $t$를 사용해 다음처럼 보간된다. 이를 구체 선형보간(spherical linear interpolation, slerp)라고 부른다.
$\frac{\sin\left( \phi \left( 1 - t \right) \right)}{\sin \phi}\mathbf{q} + \frac{\sin\left( \phi t \right)}{\sin \phi}\mathbf{r}$
$\phi$는 $\mathbf{q}$와 $\mathbf{r}$ 사이의 각도다.
$\mathbf{q}$와 $\mathbf{r}$의 내적은 $\left(q_x, q_y, q_z, q_w\right) \cdot \left(r_x, r_y, r_z, r_w\right) = q_xr_x + q_yr_y + q_zr_x + q_wr_w$ 또는 $\left\| \mathbf{q} \right\|\left\| \mathbf{r} \right\|\cos\phi$로 정의된다.
후자의 경우, $\left\| \mathbf{q} \right\| = \left\| \mathbf{r} \right\| = 1$이므로, $\cos\phi$와 같다.
따라서 $q_xr_x + q_yr_y + q_zr_x + q_wr_w = \cos\phi$이고, $\phi = \arccos\left( q_xr_x + q_yr_y + q_zr_x + q_wr_w \right)$가 된다.
참고
구체 선형보간 - 증명

모든 가능한 쿼터니언을 모으면 4차원 단위 구체(unit sphere)가 형성된다.
왼쪽 사진은 단위 구체 상의 두 쿼터니언 $\mathbf{q}$와 $\mathbf{r}$을 보여준다.
$\mathbf{q}$와 $\mathbf{r}$을 보간한 쿼터니언은 이들을 잇는 최단 거리 호(shortest arc) 위에 존재해야 한다.
오른쪽 그림은 4차원 단위 구체의 단면이다. 이는 $\mathbf{q}$와 $\mathbf{r}$에 의해 정의된 대원(great circle)이다.
$\mathbf{q}$와 $\mathbf{r}$을 보간한 쿼터니언을 $\mathbf{s}$로 표기하면, 평행사변형 법칙에 따라 다음과 같이 정의된다.
$\mathbf{s} = l_1\mathbf{q} + l_2\mathbf{r}$
$\sin\phi = \frac{h_1}{l_1}$이므로 $l_1 = \frac{h_1}{\sin\phi}$이다.
또한, $h_1 = \sin\left( \phi\left( 1-t \right) \right)$이므로 다음 식을 유도할 수 있다.
$l_1 = \frac{\sin\left( \phi \left( 1-t \right) \right)}{\sin\phi}$
같은 방식으로 $l_2$도 다음과 같이 계산된다.
$l_2 = \frac{\sin\left( \phi t \right)}{\sin\phi}$
$l_1$, $l_2$에 각각 대입하면 다음과 같은 수식을 얻을 수 있다.
$\frac{\sin\left( \phi \left( 1 - t \right) \right)}{\sin \phi}\mathbf{q} + \frac{\sin\left( \phi t \right)}{\sin \phi}\mathbf{r}$
11.3.4 쿼터니언과 회전 행렬
쿼터니언 $\left( q_x, q_y, q_z, q_w \right)$가 주어졌을 때, 이를 회전 행렬로 전환하면 다음과 같다.

역으로, 회전 행렬이 주어졌을 때, 쿼터니언을 계산하는 것도 가능하다.
참고
쿼터니언에서 회전 행렬로의 전환
두 개의 쿼터니언의 곱인 $\mathbf{pq}$의 네 개 원소는 모두 $p_x, p_y, p_z, p_w$의 선형조합(linear combination)이므로, $\mathbf{pq}$는 행렬과 벡터의 곱으로 표현할 수 있다.
한편, $\mathbf{pq}$의 네 개 원소는 $q_x, q_y, q_z, q_w$의 선형조합이기도 하므로, $\mathbf{pq}$는 다음과 같이 표현할 수도 있다.
$\mathbf{qpq}^*$로 표현된 회전은 다음과 같이 정리된다.
$M_{\mathbf{q^*}}N_{\mathbf{q}}$는 쿼터니언 회전 행렬 $\mathbf{M}$처럼 정리된다.
회전 행렬에서 쿼터니언으로의 전환
주어진 회전 행렬을 쿼터니언으로 전환하는 것은 $\mathbf{M}$에서 $q_x, q_y, q_z, q_w$를 추려내는 것과 같다.
$\mathbf{M}$의 대각 원소 모두를 합한 것을 $tr\left( \mathbf{M} \right)$이라 하면, 다음과 같이 된다.

이로부터 쿼터니언의 실수부 $q_w$는 $\pm \frac{\sqrt{tr\left(\mathbf{M}\right)}}{2}$로 계산된다.
$\mathbf{M}$의 두 원소 $m_{21} = 2 \left( q_xq_y + q_wq_z\right)$와 $m_{12} = 2\left( q_xq_y - q_wq_z \right)$의 차이는 다음과 같다.

$q_z$는 $\frac{\left( m_{21} - m_{12} \right)}{4q_w}$이다. 같은 방식으로 $q_x$와 $q_y$를 구할 수 있다.
즉, $q_x = \frac{\left( m_{32} - m_{23} \right)}{4q_w}$이고 $q_y = \frac{\left( m_{13} - m_{31} \right)}{4q_w}$이다.
이렇게 얻은 $\left(q_x,q_y,q_z,q_w \right)$를 $\mathbf{q}$라 표기하자.
$q_w$가 양수와 음수 두 가지 값을 가지므로, $\mathbf{q}$와 $-\mathbf{q}$도 $\mathbf{M}$으로부터 얻어진 쿼터니언이 된다. 따라서 두 쿼터니언은 동일한 회전을 나타낸다.
출처
[OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문]을 보고 공부하고 정리한 내용
'공부 > 컴퓨터 그래픽스' 카테고리의 다른 글
| OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 Chapter 13 캐릭터 애니메이션 (0) | 2024.07.19 |
|---|---|
| OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 Chapter 12 스크린 물체 조작 (0) | 2024.07.12 |
| OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 Chapter 10 출력 병합기 (0) | 2024.07.12 |
| OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 Chapter 09 라이팅 (0) | 2024.07.12 |
| OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 Chapter 08 이미지 텍스처링 (0) | 2024.07.07 |



